物理组：许锦荣

        一．本节学习目标：
        1.理解最高点速度的临界问题，并会建立向心力方程求解力或者运动量。
        2.理解杆—球，线—球模型在竖直平面内做的圆周运动重力对其的影响
        3.会分析任意位置的向心力来源，并建立向心力方程求解力或者运动量。

        二．重难点：两种模型中最高点的临界问题

        三．师生探究问题：
        （一）如图所示，小球的质量为m=1kg，固定在轻细直杆的一端，并随杆一起绕杆的另一端O点,在竖直平面内圆周运动，已知杆长L=10m，（g=10 )如果小球经过最高点时
        （1）小球只受重力，求小球的速度v
        （2）速度大小V=12m/s ，求杆对球的作用力
        （3）速度大小V=8 m/s ， 求杆对球的作用力

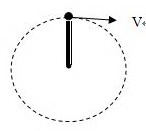
        结论：在杆-球圆周运动模型中，杆长为L，小球质量为m，在最高点位置，如果小球的速度为V，如何分析并求解杆对球的作用力F？

        （二）把上面模型中的轻细杆，换成轻绳（或细线），已知绳长为L，小球质量为m,
        如果在最高点处小球速度为V
        （1）求解一下绳上的拉力F。     

        （2）与硬杆相比，绳对小球的作用力有什么不同  
  
     
                                         
        那小球要通过最高点，对小球的速度有没有要求？

 
        （三） 用细线拴着质量为m的小球，在竖直平面内做半径为L的圆周运动，
        （1）用学过的圆周运动向心力知识求解图中该位置绳上的拉力。（已知：m  V  θ  L)

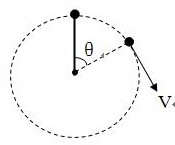
        （2）分析一下从最高点到最低点的过程中，绳上拉力的变化情况。

        （3）最低点位置，如果小球速度为V，求杆（绳）上的拉力

        （四）其它模型最高点位置速度的临界问题：
        1.在竖直平面内圆周运动的翻滚过山车，在最高点位置速度有何限定？类似于_______模型
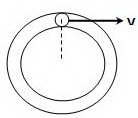
        2.同心圆环模型。类似于___________模型
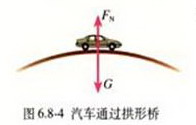
        3.汽车在拱形桥桥顶，在该位置，从安全角度考虑，对汽车的速度又有何限定？

        （五）本节知识小结：